Going beyond experimental studies based on mechanics of nanostructured materials, we worked on problems at the interface between mechanics and physics by utilizing finite element methods and experimental verifications.
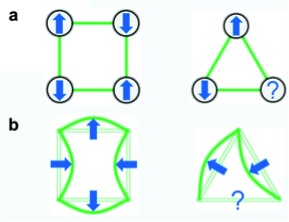
We demonstrated a system consisting of elastic beams connected to form a two-dimensional triangular lattice in which a simple and ubiquitous phenomenon such as buckling induces geometrical frustration (Physical Review Letters 2014). Geometrical frustration is a situation that a system cannot simultaneously minimize all interactions because of geometric constraints1 and it is typically characterized by disordered configurations due to degenerate ground states. The essence of this phenomenon can be easily captured by comparing a square with a triangular frame, as shown in Fig. 3. In the square frame, each beam can buckle into the most energetically favored configuration – a half sinusoid – and simultaneously preserve the angles with all its neighbors at joints to minimize the deformation. On a triangular frame such configuration is impossible, so the system becomes frustrated (Fig. 3b-right) and it is unclear what should be the buckled configuration. Interestingly, we showed both numerically and experimentally that buckling in frustrated triangular cellular structures results in the formation of complex ordered patterns.
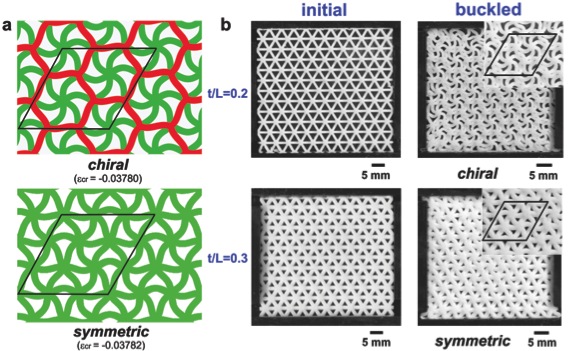
The identification of frustrated systems for which ordered configurations emerge naturally has been a fundamental challenge. Furthermore, despite decades of research on geometrical frustration, little is known about the geometrically frustrated elastic continuum structures, since most of the previous studies have focused on systems comprising discrete elements such as spins, molecules and colloids2.We have found that the connected geometry favors the formation of complex ordered symmetric or chiral patterns and the appearance of a specific configuration is controlled by the porosity of the system (Fig. 4). Our results indicate that simple changes in the geometry of the elastic structures may lead to novel effects. With intriguing and rich behavior originating from the interplay between geometry and elasticity, continuum geometrically frustrated lattice structures offer novel phenomena to be investigated.
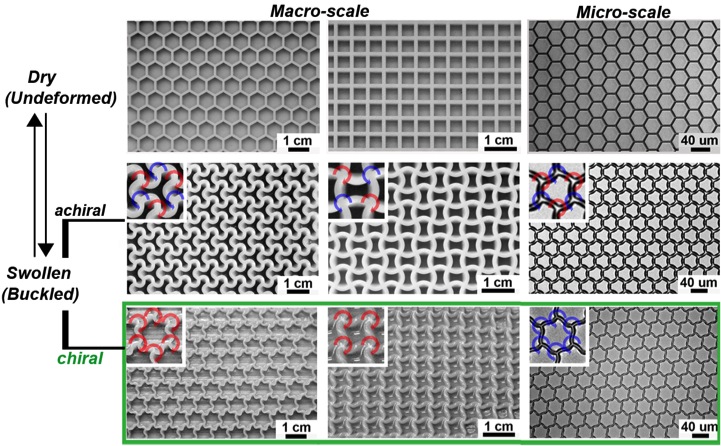
Moreover, we developed a fundamentally new way of generating chiral structures with desired handedness by exploiting buckling in supported cellular structures (Advanced Materials 2013, highlighted in Nature Physics 2013). Guided by theoretical analysis, we rationally designed cellular structures in which buckling induces a reversible switching between achiral and chiral configurations (Fig. 5). Given that the proposed mechanism is governed by a mechanical instability that is scale-independent, the principle can be generalized over a wide range of length scales, geometries, materials, and stimuli. Importantly, this scale-independent behavior allows us to scrutinize the kinetics of both the nucleation which causes the symmetry breaking, and the propagation of this chirality which is assisted by a localized self-correction mechanism to yield uniform patterns of single handedness. The full control over the chiral outcome in combination with the wealth of different length scales, materials, stimuli, and geometrical designs provides reversibly transformable architectures with a broad field of applications such as tunable sensors and switchable optical elements.
Finally, inspired by a natural mineral, Zeolite, we developed a soft periodic structure with multiple folding mechanisms and showed the first experimental demonstration of soft tunable phononic crystals (Advanced Functional Materials 2014). In this system, multiple modes and corresponding band gaps can be triggered by changing the horizontal and the vertical strain ratio and the resulting deformation behaviors and dispersion relations showed good agreement between numerical simulations and experiments providing a versatile device for controlling wave propagation.
References
1 Han, Y. et al. Geometric frustration in buckled colloidal monolayers. Nature 456, 898–903 (2008).
2 Sadoc, J.-F. S. & Mosseri, R. Geometrical Frustration (Cambridge University Press, 2006).